『壁』のお話 ( ̄ー ̄;)
5月には、各高校、定期考査や一斉考査が行われ、
その結果も戻ってきたと思います。
1年生にとっては入学後初めての本格的なテスト
緊張した割には「あまり大したことなかったな」
というのが大方の感想でしょう
↑
ただしこれは『罠』ですからね ( ̄▽ ̄)
まあその『罠』の話はまた今度にするとして
この時期よく聞かれるのは高校2年生からの
「1年のときは数学よかったんだけど
1年の終りから最近調子が悪いんだよね」
といった言葉。

これって、みんな意外と気づいていないんですよね。
ということで、今回の動画のテーマは
高校2年生が知っておくべき
をお送りします。よろしかったらご覧ください。
その結果も戻ってきたと思います。
1年生にとっては入学後初めての本格的なテスト
緊張した割には「あまり大したことなかったな」
というのが大方の感想でしょう
↑
ただしこれは『罠』ですからね ( ̄▽ ̄)
まあその『罠』の話はまた今度にするとして
この時期よく聞かれるのは高校2年生からの
「1年のときは数学よかったんだけど
1年の終りから最近調子が悪いんだよね」
といった言葉。

これって、みんな意外と気づいていないんですよね。
ということで、今回の動画のテーマは
高校2年生が知っておくべき
『数学ⅡBの壁』
をお送りします。よろしかったらご覧ください。
まあ、原因さえわかれば、対処できますからね( ̄▽ ̄)v
あとは皆さんの努力あるのみです。
以上 学長でした。
『人間、辛抱だ。』
「土俵の鬼」と呼ばれた元横綱初代若乃花と
元大関貴ノ花の兄弟が1970年代に出演した
テレビCMで使われたセリフ
『人間、辛抱だ。』
いや~実に奥が深い ( ̄ー ̄)
今日はこの言葉をそのまま受験生に送りましょう‼
ということで 今回の動画はこちら
受験勉強に『挫折』しないために知っておくべきこと
よろしかったらご覧ください。
よろしかったらご覧ください。
ー---------キリトリー---------
ちなみに木村拓哉さん主演の『栄光への10カウント』
いろいろ言われているようですが
私はおもしろく観ています ( ̄▽ ̄)
今度「キムタク」に対抗する動画作ってみようかな・・・
あっ 石は投げないで~~~
以上、学長でした。
◯◯◯◯ 始めました〜♬
まあ少しずつ暑くなってきましたので
↑
誰かさんがブログサボってる間にねd( ̄  ̄)
↑
この時期、始めるものといえば『冷やし中華』ですが、
教室で『冷やし中華』作っても仕方がないので
受験情報に関する
“YouTube” を始めました‼︎
↑
誰かさんがブログサボってる間にねd( ̄  ̄)
↑
(;一_一)
この時期、始めるものといえば『冷やし中華』ですが、
教室で『冷やし中華』作っても仕方がないので
受験情報に関する
“YouTube” を始めました‼︎
大学受験・高校受験に関する情報をお送りします‼
YouTuber になったわけではないので『チャンネル登録』は必要ないですよ(笑)
ただブログ並みに(ブログ以上に?)不定期になる可能性があるので、登録しておけば見逃しはないでしょうけどね。
以上 学長でした
やはり逃げるのか~~!!
1月は「行く」
2月は「逃げる」
誰が言ったか知りませんが
まさにその通りです ( ̄◇ ̄;)
共通テストが終わったと思えば
今週末には もう国公立大学の前期試験が・・・
今年も 国立の2次対策を終え
2月は「逃げる」
誰が言ったか知りませんが
まさにその通りです ( ̄◇ ̄;)
共通テストが終わったと思えば
今週末には もう国公立大学の前期試験が・・・
今年も 国立の2次対策を終え
受験生を送り出すことができました
あとは皆さんの健闘を祈るのみ
祈ることぐらいしかできません
無事 全力を出し切ることができますように

以上 学長でした
祈ることぐらいしかできません
無事 全力を出し切ることができますように

以上 学長でした
共通テスト⑥【数学ⅡB・後半】
やっとたどり着きました。共通テスト数学(最終回)です。
昨日もお話しした通り、解いた内容をすでに忘れている・・・
仕方がないので、朝から数Bだけもう一度解いた「白ヤギ」さんです。
第3問 [確率分布と統計的な推測]
(1)は目をつぶってでも取れるような「2項分布」の基礎の基礎。
(2)は(1)の2項分布を正規分布→標準正規分布と引き直し、ある確率になる標本比率の範囲を求めるオーソドックスな問題。
(3)はめずらしく『確率密度関数』に関する問題であった。さらにその確率密度関数が『1次関数』で与えられているので、そこで戸惑った人もいたかもしれない。しかし、定石通り100≦x≦200における台形の面積を求めればよいことに気づけば容易に問題は解決できる。
ちなみに、ほとんどの高校では「確率分布」を履修しないようであるが、「ベクトル」「数列」を苦手とする文系の生徒などは「確率分布」を選択するのもありだと思う。実際、今年も「ベクトル」がどうしてもダメだという生徒に「確率分布」を一から教えたら、それなりに得点してきていた。
第4問 [数列]
『問題文が長すぎる』とやり玉に挙げられている問題。問題の内容を分かりやすくするために、少し言葉を変えて紹介する。
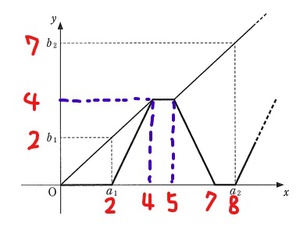
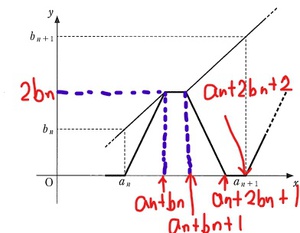
「弟が家を出て一定の速さで学校に向けて歩いている。弟が家を出て2分後、兄が自転車で弟の歩く速さの2倍の速さで弟を追いかける。兄が弟に追いつくと1分間立ち止まって話をした後、弟は同じ速さで再び学校に向け歩き出し、兄も同じ速さで自転車で家に戻る。家に帰り着いた兄は1分間休憩したのち、再び家を出て弟を追いかける。このことを何度も繰り返し、兄は家と弟の間を何度も往復する。」
これって、どんな状況なの? 「『日常の事象』を題材にして」とか言うけど、全然日常的じゃないんですけど。
ちなみに、私はこんな感じで解きました。
第3問 [確率分布と統計的な推測]
(1)は目をつぶってでも取れるような「2項分布」の基礎の基礎。
(2)は(1)の2項分布を正規分布→標準正規分布と引き直し、ある確率になる標本比率の範囲を求めるオーソドックスな問題。
(3)はめずらしく『確率密度関数』に関する問題であった。さらにその確率密度関数が『1次関数』で与えられているので、そこで戸惑った人もいたかもしれない。しかし、定石通り100≦x≦200における台形の面積を求めればよいことに気づけば容易に問題は解決できる。
ちなみに、ほとんどの高校では「確率分布」を履修しないようであるが、「ベクトル」「数列」を苦手とする文系の生徒などは「確率分布」を選択するのもありだと思う。実際、今年も「ベクトル」がどうしてもダメだという生徒に「確率分布」を一から教えたら、それなりに得点してきていた。
第4問 [数列]
『問題文が長すぎる』とやり玉に挙げられている問題。問題の内容を分かりやすくするために、少し言葉を変えて紹介する。
「弟が家を出て一定の速さで学校に向けて歩いている。弟が家を出て2分後、兄が自転車で弟の歩く速さの2倍の速さで弟を追いかける。兄が弟に追いつくと1分間立ち止まって話をした後、弟は同じ速さで再び学校に向け歩き出し、兄も同じ速さで自転車で家に戻る。家に帰り着いた兄は1分間休憩したのち、再び家を出て弟を追いかける。このことを何度も繰り返し、兄は家と弟の間を何度も往復する。」
これって、どんな状況なの? 「『日常の事象』を題材にして」とか言うけど、全然日常的じゃないんですけど。
ちなみに、私はこんな感じで解きました。


なんか高校入試で出題される「一次関数の利用」の問題を解いているような感じがしました
そしてこのあと『2項間漸化式』に入り、ようやく高校数学『数列』の問題になっていくんですが、そこまで辿り着いた人がどれだけいたことか・・・
(ある生徒との「笑えない」会話) 生徒:数列は「漸化式」がでると思ってたんですけどね 私:「漸化式」出てたじゃん 生徒:えっ?
第5問 [ベクトル]
(1)条件を丁寧に代入していけば、文字式だけでも正解に達することができる基本的な問題(もちろん図は描くべきですが)。
(2)ここはしっかりとした図を描かなければイメージもわかず、正解するのは難しいでしょう。しかし、ここで図を描ければこの後がとても楽になります。
(3)(2)の図に基づいて点Rの位置をとらえれば、計算は比較的楽だと思う。
やはり(2)の図がしっかり描けるか否かが分かれ道だったか。
ⅠA・ⅡBを通して改めて感じたことは
①やはり数学の問題で勝負しましょう。数学以外のことを共通テストに負わせるのは場違いだと思います。
②無駄な文章をダラダラ書くぐらいなら、もっと幅広く基本事項を問いましょう。限られた狭い項目しか聞いていない設問が多かったように思います。
③誘導をもう少し工夫してもらいたい。誘導が雑なので「パタッ」と受験生の手が止まってしまうところも多々あったと思います。
来年は改善されることを願っています。
今年の受験生諸君。受験はこれからです。最後まで粘り抜いてください!!
以上、学長でした。
長々と申し訳ありませんでした(;一_一)
共通テスト⑤【数学ⅡB・前半】
数学ⅡBは『数列』などの問題文の長さがよく取り上げられるが、前半のⅡは比較的平易な問題だったと思う。ただ、『ⅠAショック』を受けた受験生が、精神的にどこまで立て直すことができたか。「羹に懲りて膾を吹く」ことなく、客観的に問題を見ることができたか。意外とそのあたりで差が付いたかもしれない。
「図形と方程式」に「三角関数」を少し盛り込んだ問題。
(1)は円の方程式を変形して中心と半径を求め、不等式の領域を求めるだけの超基本的な問題。こんな問題から入れると受験生も安心しますよね。
(2)は円外の点を通る直線と円が共有点を持つための条件を求める問題。「判別式を用いた解法」と「tanを用いた解法」でアプローチさせている。私は個人的に「太郎さん・花子さん問題」が嫌いだが、このように一つの問題に対して複数のアプローチを考えさせる問題は良いと思う。特に今回は最近主流の「点と直線の距離による解法」を外しているのも良い。受験生は「チャート」や「レジェンド」などで勉強する際に『別解』も理解するように努めてもらいたい。
第1問 [2]
(1)は円の方程式を変形して中心と半径を求め、不等式の領域を求めるだけの超基本的な問題。こんな問題から入れると受験生も安心しますよね。
(2)は円外の点を通る直線と円が共有点を持つための条件を求める問題。「判別式を用いた解法」と「tanを用いた解法」でアプローチさせている。私は個人的に「太郎さん・花子さん問題」が嫌いだが、このように一つの問題に対して複数のアプローチを考えさせる問題は良いと思う。特に今回は最近主流の「点と直線の距離による解法」を外しているのも良い。受験生は「チャート」や「レジェンド」などで勉強する際に『別解』も理解するように努めてもらいたい。
第1問 [2]
指数関数・対数関数の問題
(1)(2)ともに対数の計算(定義)・対数方程式など基本知識を問う問題。
(3)対数不等式についての問題だが、誘導の仕方には評価が分かれるところではなかろうか。
(4)単独でも十分正解に達することができる。
第2問 [1]
微分に関する問題
(1)3次関数について、f'(x)=0の解の個数からグラフの概形を読み取るのは必須。4次関数でf'(x)=0が2重解を持つ場合などもグラフの概形が読み取れるようになっておいてもらいたいところ。
(2)前半はちょっと計算が煩わしく感じた人もいるかもしれないが、内容は極めて基本的な問題。後半は、3次関数の点対称性を用いると瞬殺ですね。
(3)ここは一転「必要性」と「十分性」をきく、コンパクトだが良い問題だと思う。
第2問 [2]
積分に関する問題
小問構成はなし。
前半は2つの3次関数の位置関係から、囲まれた部分の面積を求めるための式を選ぶ問題。3次曲線の位置関係と基本事項が理解できていれば問題なく取れる。
後半は、前半で出した式を実行するだけ。ただ、少々計算が面倒で特に最後のtについての3次方程式は因数定理の「代入する値」が理解できていないと出せないでしょう。得点調整的な設問のイメージを感じました。
私は、解いた問題を解いたそばから忘れていく。
ましてや1週間前に解いた問題など、自分が計算して解いた痕跡を見ても思い出せない時がある。
まさに「こんな問題説いたっけ?」状態である←昔からだから歳のせいではない( ̄- ̄)
ただ本当に情けない( ̄◇ ̄;) こんな私でも何とかなってるんですから、受験生の皆さん頑張ってください。
以上 学長でした
共通テスト④【数学ⅠA・後半】
今日は前回の続き、ⅠAの後半をやります。
第3問(確率)
プレゼント交換で、全員自分以外の人が持って来たプレゼントを受け取る、いわゆる『完全順列』の問題。
ちなみに「〇〇の問題」のように問題にラベリングを行って「解法」と結びつけるのは、効率よく学習する上で有効だと思います。
第3問(確率)
プレゼント交換で、全員自分以外の人が持って来たプレゼントを受け取る、いわゆる『完全順列』の問題。
ちなみに「〇〇の問題」のように問題にラベリングを行って「解法」と結びつけるのは、効率よく学習する上で有効だと思います。
(1)プレゼントを交換する人数を、2人、3人、4人と増やしていき確率を求めさせる。ちなみに、2人でプレゼントの交換を行う場合、例えば恋人同士がプレゼントの交換を行うとき、このような交換会を行うか?日常生活に則した問題というが、誰もツッコまなかったのだろうか?まあ受験生は1問分儲かったので良しとしておこう。
(2)4人で交換会を行うとき、全員が自分以外のプレゼントを受け取る確率を求めさせる問題。余事象を用いるように誘導されているのだが、正解が3/8となっていることからも分かる通り、余事象を用いない方が楽だと思う。
(3)5人になるのだが(2)の解法を参考にしろということなのだろうか?はっきり言って「嫌だ」。理由「めんどくさいから」。生徒が持って来たどこかの予備校の問題で、4人が交換したところに5人目が現れてさらに交換するというのがあったが、そちらの方がはるかに「数学的」に意義があるように私は感じた。
(4)条件付確率の問題で特に問題はないか。

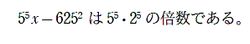
第5問(図形の性質)
重心の性質・メネラウスの定理・方べきの定理など、基本的な知識を試すオーソドックスな問題だったと思います。「比の合成」はできれば中学の段階で身に着けておいてもらえるといいですよね。
第4問(整数の性質)
1次不定方程式の問題である。最初でつまずくと全滅する問題。選択問題なので他をあたってもらいたい。

(1)まずは係数が指数になっているのを見て「えっ」とちょっと怯んだ生徒もいたかもしれない。
「このことを用いると」→「どうやって用いるんだよ~」 手を動かさずに悩んだ人もいるかもしれない。
(2)(1)の式を移行して両辺2乗するだけなのだが、ここでパタッと止まった生徒もけっこういたようだ。
(3)誘導の文はどうなのだろうか?実は
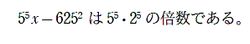
この部分からだけで、答えは出せるんですよね。一応。
(4)もういい、お腹いっぱい。整数の問題って「1次不定方程式」だけでしたっけ?
重心の性質・メネラウスの定理・方べきの定理など、基本的な知識を試すオーソドックスな問題だったと思います。「比の合成」はできれば中学の段階で身に着けておいてもらえるといいですよね。
いかん、昼間っから2次試験対策もあるので、そろそろバテてきた(;一_一)
↑
ご存じの通り また「伏線」か?
期待されてなくても頑張ります!! 次回はⅡBの前半を!!
↑
問題は「次回」がいつかだな( ̄▽ ̄)
以上、学長でした。
共通テスト③ 【数学ⅠA・前半】
今日こそは「数学的に」「各論」を。
解いたとき、最初に感じたのは
「トントン パタッ トントン パタッ」 だな・・・
意味不明に聞こえるでしょうね(笑)
調子よく「トントン」と解いていると、急に「えっナニコレ?」というのが出てきて「パタッ」と手が止まる。
落ち着いて『俯瞰的に』見れば突破口が見つかるのだが、極度の緊張感の中では『焦り』を引き起こす。
前置きはそのくらいで内容へ
【第1問】 [1]
基本対称式を用いた問題であるが、文字2つ→文字3つという展開が通常の出題パターンのように思うが、いきなり文字3つから入っていた。ただ内容は極めて平易で問題はない。(2)で「(1)の計算から」という親切な誘導があり、これを活かせれば即決。気づかなくとも力技で何とかなるが、時間を浪費する。やはり人の親切は素直に受け入れるべきである。
【第1問】 [2]
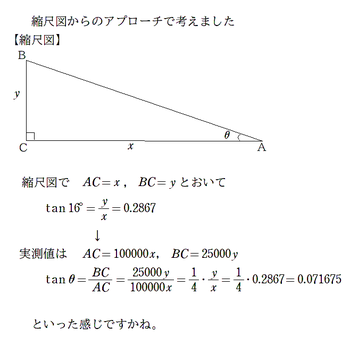
最初の「パタッ」はここだったかなと思う。「三角比の表」を使わせたいのだろうが、縮尺の誤りといった設定に何の意味があるのだろうか?「地理」か「地学」ででもやってもらいたい。「ここで詰まったんですよ」という生徒と「いやそこはすんなりといけました」という生徒に分かれていた。ちなみに私はこのように考えた。

【第1問】 [3]
(1)は問題なく「トントン」と解ける。(2)のABの範囲を求めるところで「パタッ」と止まる。ここで完全に止まった生徒も多かった。ABもACも「外接円の直径より長くはなりようがない」ということに気づけば切り抜けられる。ただ、それに気づいた生徒でも「それだけでいいのか?」と思案してしまったようである(良い思案なんだけどなぁ)。しっかり勉強している生徒ほど時間を使ってしまったかもしれない。
個人的には、問題全体を見渡せば、ABの範囲に関係なく次の「ADをABで表す問題」は(1)と同様の方法で解けるので、そこは拾ってもらいたかった。
【第2問】 [1]
(1)(2)は特に問題ないように思えた。が、これって数Ⅱで頻出の「3次方程式が2重解をもつ」という問題と発想が同じではないのか?まあかまわないが。
(3)は2次関数においてxの係数はグラフの「軸」に、定数項は頂点のy座標に影響を与えることからサクッと処理してもらいたい。
(4)は「『内側』ならば『外側』」を使うために、③と④の「動かないところ」と「共有点」に留意してグラフを描いてもらえればクリアできる。はずだが、ここで「パタッ」となった生徒は多かった。x軸との共有点が必要と考えたのだろう。
【第2問】 [2]
(1)は現行の学習指導要領では、高校入試に出題さる可能性もある問題ではなかろうか。『ス』の判断さえ慎重に行えば特に問題はない、「トントン」の問題である。
(2)は丁寧に照らし合わせれば確実に正解にたどり着くことができる。しかし、丁寧にやりすぎると知らず知らずのうちに時間を取られてしまう。このようなところで意外と時間を浪費する危険性があるので、選択肢の散布図からその特徴的な違いを押さえたうえで確認するのが効率的である。
(3)単に「相関係数の公式」を覚えているかどうか。効率よく小数の計算ができるかどうか。ただそれだけの問題。
(4)相関係数の0.63という値で①か③ということになるとは思うのですが,あとは平均値からのばらつきで③と判断するしかなさそうですね.
われながら「なんと『ざっくり』な‼」 と思ってはいますが
懲りずに次回はⅠA(後半)の予定です。
以上、学長でした。
共通テスト数学②
( ̄◇ ̄;)( ̄◇ ̄;)( ̄◇ ̄;)( ̄◇ ̄;)( ̄◇ ̄;)
・・・いや~ありがたいです
ということで久々の
ーーーーーーーーーーキリトリーーーーーーーーーー
『総論』の摘み残し(話し残し?)がありましたので、その話を少し。
高校受験にも参考になるのでご容赦ください。

そもそも「2年目のジンクス」ではないですが、今年の共通テストは『難化する』と言われていました。
ですから生徒たちには、難化したときの対応の仕方、いわゆる『逃げ方』についても、
「ちょっとくどくない?」と思われるくらい、あらかじめ話しをしておきました。
その結果、「先生、数学やらかしちゃいました・・・」と報告に来てくれた生徒の結果を見ても
「いや、うまく逃げ切れてる。いけると思うよ」
実際、第一志望校A・B判定で、そのままGOサインを出す生徒は多かったですね。
また本番1か月前、高校での問題演習で散々な点数しか取れていなかった文系の生徒に
「取れるところを見つけ出し、確実に取る」といったトレーニングをしたところ
決して高い点数ではありませんが、国立大を十分ねらえるくらいの得点を『もぎ取ってきた』生徒もいました。
つまり今年のように、特定の科目の難易度が極端に上がったテストの場合
①他の科目をしっかり取る(悪い結果を引きずらない)。
②難しいなりに、取れるところで1点でも多く取る。
といった「当たり前」のことを当たり前にできるかどうかにかかってきます。
逆に数学が得意で、ここで点数を稼いでおきたい生徒
逆に数学が得意で、ここで点数を稼いでおきたい生徒
「最低9割、できれば満点」と目論んでいる生徒は深手を負いやすい。
このような生徒は、1問・2問の取りこぼしが致命傷と考えているので、
解けない問題にあたると必要以上に時間を費やしてしまいます。
それでも解ければ少し良いのですが、解けないとなると、
「時間がない」「もう落とせない」といった焦りの悪循環に突入し、
普段なら考えられないようなミスを連発していきます。
高校受験の場合にも、まったく同じことが言えます。
高校受験の場合にも、まったく同じことが言えます。
私は「数学」が得意な生徒でも、目標点を90点には設定させません。
5教科の中で「数学」だけは『守りの教科』であることを理解させ、
最低80点を確保することを目標とさせます。
そして、80点を確保するには20点分・5分の1の失点が許されることを意識させます。
その結果、上手く事が運び90点以上を得点できるのは良いですが、
70点・60点と大きく崩れることだけは防がなければなりません。
『難化』したときには『難化』したときなりの乗り越え方はあります。
念のため申し上げておきますが、昨日のブログで私が言いたかった(怒っていた)のは、
『難化』したこと自体に対してではなく、『難化の仕方』に問題があったということなのです。
言い訳じみたことを長々と述べてしまい申し訳ございません。
次回は、必ず「各論」に入ります。
以上、学長でした。
【怒】共通テスト数学①
初回は『総論』を。
当然、日曜の夜と月曜日に分け、私も解いてみた。
正直、『数学的に』そこまで難しい問題ではなかった。
ただ、解いているときに感じたことは、
「みんなやられてるだろうな。平均点激下がりか・・・」
結果は皆さんご存じの通り、大幅な平均点の低下。
数学ⅠAに至っては過去最低の38点だった。
そこまで難しくなかったのに
『なぜ高校生は得点できなかったのか?』
末松文部科学大臣 21日のコメント
「全体的に暗記型ではなく、日常生活の場面を題材にした問題や、様々な資料や図から複数の情報を読み取って活用する能力を問う問題がより明確になっている。」
もちろん「数学」についてのみの感想ではないのだが、「数学」の出題を強く意識していることは感じ取れる。
『日常生活の場面を題材にした問題や、様々な資料や図から複数の情報を読み取って活用する能力』を問いたい。
一万歩ほど譲歩してこの方向性を認めたとしても、今回の最大の問題点はここにある。
「そのような能力を試したいのであれば、現行の教科書はそのような能力を十分身に着けさせることができるものとなっているのか?」
「多くの公立の高校でそのような能力を身に着けさせる指導がなされているのか?」
文部科学省として、そのような体制を十分整えることもなく、高校生に対してだけ能力を要求している。
高校生はあなたたちの実験台ではない!!

「暗記型」だけではなく、などと軽々しく言うが、
三角関数・指数関数・対数関数・微分・積分・ベクトル・数列・複素数・・・
高校数学で登場する新しい数学的概念だけでも、結構な量がある。
そしてこれらに伴う「公式」や「解法」、それらをマスターするだけでもどれだけの労力を必要とすることか。
教科は数学だけではない。英語や理科もある。
高校生活は勉強だけではない。部活や生徒会の活動などもある。
そのような状況の中、数学の基礎力を身につけた上で更なる活用力を身につけろというのか。
今回解いてみて「難しくはない」と感じた。
なぜか? 解いているとき使っていたのは頭の中の『数学的な』部分ではなく、主に『事務処理的な』部分を使ったからだ。
「数学の問題を解く」のではなく「仕事の事務を処理する」感覚で解くと、意外と楽に解ける。
念のために言っておくが、それは『問題解決能力』などといった高度なものではなく、単なる『事務処理能力』である。
当然普通の高校生が身に着けているものではなく、脳が若々しい貴重な高校時代に、数学を通して身に着けるべきようなものでもない。
今回のテストでおかしいところはまだまだある。
ただ、最大の『罪』は、「受験生の努力を正当に評価できなかった」ことにある。
人の努力を、懸命な努力を踏みにじるような問題を平気で出題したことである。
誰かが責任を取るべきレベルの問題である。
「たかが入試問題で」と思われるかもしれないが、
日々彼らの努力を目にしてきた者として、看過できないことである。
『総論』が長くなってしまった(言いたいことはまだまだあるが)。
次回は、『各論』を具体的に、できれば『数学的』に。
以上、学長でした。







