共通テスト③ 【数学ⅠA・前半】
今日こそは「数学的に」「各論」を。
解いたとき、最初に感じたのは
「トントン パタッ トントン パタッ」 だな・・・
意味不明に聞こえるでしょうね(笑)
調子よく「トントン」と解いていると、急に「えっナニコレ?」というのが出てきて「パタッ」と手が止まる。
落ち着いて『俯瞰的に』見れば突破口が見つかるのだが、極度の緊張感の中では『焦り』を引き起こす。
前置きはそのくらいで内容へ
【第1問】 [1]
基本対称式を用いた問題であるが、文字2つ→文字3つという展開が通常の出題パターンのように思うが、いきなり文字3つから入っていた。ただ内容は極めて平易で問題はない。(2)で「(1)の計算から」という親切な誘導があり、これを活かせれば即決。気づかなくとも力技で何とかなるが、時間を浪費する。やはり人の親切は素直に受け入れるべきである。
【第1問】 [2]
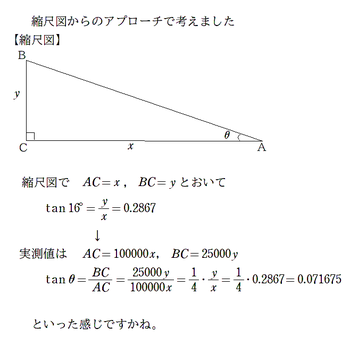
最初の「パタッ」はここだったかなと思う。「三角比の表」を使わせたいのだろうが、縮尺の誤りといった設定に何の意味があるのだろうか?「地理」か「地学」ででもやってもらいたい。「ここで詰まったんですよ」という生徒と「いやそこはすんなりといけました」という生徒に分かれていた。ちなみに私はこのように考えた。

【第1問】 [3]
(1)は問題なく「トントン」と解ける。(2)のABの範囲を求めるところで「パタッ」と止まる。ここで完全に止まった生徒も多かった。ABもACも「外接円の直径より長くはなりようがない」ということに気づけば切り抜けられる。ただ、それに気づいた生徒でも「それだけでいいのか?」と思案してしまったようである(良い思案なんだけどなぁ)。しっかり勉強している生徒ほど時間を使ってしまったかもしれない。
個人的には、問題全体を見渡せば、ABの範囲に関係なく次の「ADをABで表す問題」は(1)と同様の方法で解けるので、そこは拾ってもらいたかった。
【第2問】 [1]
(1)(2)は特に問題ないように思えた。が、これって数Ⅱで頻出の「3次方程式が2重解をもつ」という問題と発想が同じではないのか?まあかまわないが。
(3)は2次関数においてxの係数はグラフの「軸」に、定数項は頂点のy座標に影響を与えることからサクッと処理してもらいたい。
(4)は「『内側』ならば『外側』」を使うために、③と④の「動かないところ」と「共有点」に留意してグラフを描いてもらえればクリアできる。はずだが、ここで「パタッ」となった生徒は多かった。x軸との共有点が必要と考えたのだろう。
【第2問】 [2]
(1)は現行の学習指導要領では、高校入試に出題さる可能性もある問題ではなかろうか。『ス』の判断さえ慎重に行えば特に問題はない、「トントン」の問題である。
(2)は丁寧に照らし合わせれば確実に正解にたどり着くことができる。しかし、丁寧にやりすぎると知らず知らずのうちに時間を取られてしまう。このようなところで意外と時間を浪費する危険性があるので、選択肢の散布図からその特徴的な違いを押さえたうえで確認するのが効率的である。
(3)単に「相関係数の公式」を覚えているかどうか。効率よく小数の計算ができるかどうか。ただそれだけの問題。
(4)相関係数の0.63という値で①か③ということになるとは思うのですが,あとは平均値からのばらつきで③と判断するしかなさそうですね.
われながら「なんと『ざっくり』な‼」 と思ってはいますが
懲りずに次回はⅠA(後半)の予定です。
以上、学長でした。





