共通テスト④【数学ⅠA・後半】
今日は前回の続き、ⅠAの後半をやります。
第3問(確率)
プレゼント交換で、全員自分以外の人が持って来たプレゼントを受け取る、いわゆる『完全順列』の問題。
ちなみに「〇〇の問題」のように問題にラベリングを行って「解法」と結びつけるのは、効率よく学習する上で有効だと思います。
第3問(確率)
プレゼント交換で、全員自分以外の人が持って来たプレゼントを受け取る、いわゆる『完全順列』の問題。
ちなみに「〇〇の問題」のように問題にラベリングを行って「解法」と結びつけるのは、効率よく学習する上で有効だと思います。
(1)プレゼントを交換する人数を、2人、3人、4人と増やしていき確率を求めさせる。ちなみに、2人でプレゼントの交換を行う場合、例えば恋人同士がプレゼントの交換を行うとき、このような交換会を行うか?日常生活に則した問題というが、誰もツッコまなかったのだろうか?まあ受験生は1問分儲かったので良しとしておこう。
(2)4人で交換会を行うとき、全員が自分以外のプレゼントを受け取る確率を求めさせる問題。余事象を用いるように誘導されているのだが、正解が3/8となっていることからも分かる通り、余事象を用いない方が楽だと思う。
(3)5人になるのだが(2)の解法を参考にしろということなのだろうか?はっきり言って「嫌だ」。理由「めんどくさいから」。生徒が持って来たどこかの予備校の問題で、4人が交換したところに5人目が現れてさらに交換するというのがあったが、そちらの方がはるかに「数学的」に意義があるように私は感じた。
(4)条件付確率の問題で特に問題はないか。

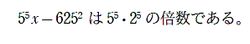
第5問(図形の性質)
重心の性質・メネラウスの定理・方べきの定理など、基本的な知識を試すオーソドックスな問題だったと思います。「比の合成」はできれば中学の段階で身に着けておいてもらえるといいですよね。
第4問(整数の性質)
1次不定方程式の問題である。最初でつまずくと全滅する問題。選択問題なので他をあたってもらいたい。

(1)まずは係数が指数になっているのを見て「えっ」とちょっと怯んだ生徒もいたかもしれない。
「このことを用いると」→「どうやって用いるんだよ~」 手を動かさずに悩んだ人もいるかもしれない。
(2)(1)の式を移行して両辺2乗するだけなのだが、ここでパタッと止まった生徒もけっこういたようだ。
(3)誘導の文はどうなのだろうか?実は
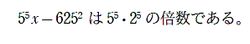
この部分からだけで、答えは出せるんですよね。一応。
(4)もういい、お腹いっぱい。整数の問題って「1次不定方程式」だけでしたっけ?
重心の性質・メネラウスの定理・方べきの定理など、基本的な知識を試すオーソドックスな問題だったと思います。「比の合成」はできれば中学の段階で身に着けておいてもらえるといいですよね。
いかん、昼間っから2次試験対策もあるので、そろそろバテてきた(;一_一)
↑
ご存じの通り また「伏線」か?
期待されてなくても頑張ります!! 次回はⅡBの前半を!!
↑
問題は「次回」がいつかだな( ̄▽ ̄)
以上、学長でした。





